Ai8051U 井字棋AI —— 人工智能之深度搜索
小姚与你在进行一个游戏,你应该怎样夺得游戏胜利?
人工智能的序幕已经拉开,是时候拼上新一块拼图了。
在人工智能领域,神经网络常常用于对结果的预测,搜索算法常用于解决决策问题,搜索算法也是人工智能图景不可或缺的一块拼图。
博弈与博弈树
零和博弈
试想一个这样的场景:小姚与你在玩“剪刀、石头、布”游戏,假设小姚获胜你的收益是-1,平局是0,你获胜是1。那么可以画出这样一个矩阵(横向为小姚,纵向为你),这就是你的收益矩阵
|
剪刀 |
石头 |
布 |
| 剪刀 |
0 |
-1 |
1 |
| 石头 |
1 |
0 |
-1 |
| 布 |
-1 |
1 |
0 |
你会发现,小姚和你的收益相加总是为0 —— 这就是零和博弈
零和博弈
参与博弈的各方,在严格竞争下,一方的收益必然意味着另一方的亏损,博弈各方的收益和损失相加总和永远为“0”
由于博弈是零和的,所以没必要对双方的收益进行表示,一个任意一方的收益矩阵即可表示博弈双方的收益
决策
再来试想另一个零和博弈场景:小姚与你在玩一个“蹲下、起立”游戏,如果:① 你和小姚同时蹲下,小姚获得5块钱;② 你蹲下的同时,小姚站着,你获得5块钱;③ 你站着的同时,小姚蹲着,你获得10块钱;④ 你和小姚同时站着,你获得8块钱。试试画出你的收益矩阵,仍然横向为小姚的动作,纵向为你的动作。
你会发现,这个博弈似乎存在着一个最优解。我们来仔细分析一下:
小姚并不是傻瓜,你就需要找到每种动作的最坏情况来估计一个最保守的动作 —— 蹲下的最坏收益是 -5,起立的最坏收益是 8。
蹲下的最坏情况和起立的最坏情况这两个最坏情况的最好情况是起立,这就是所谓的极小极大值
极小化极大策略
在最坏的基础上最最好的选择
极小化极大策略是零和博弈的重要原则
决策树
你与小姚的游戏中,你所获得的收益是使用收益矩阵表示的,也可以使用树来表示
还以“蹲下、起立”游戏为例,后续为了方便表述,博弈双方为甲乙。
以甲为起点,可以画出这样一棵树:
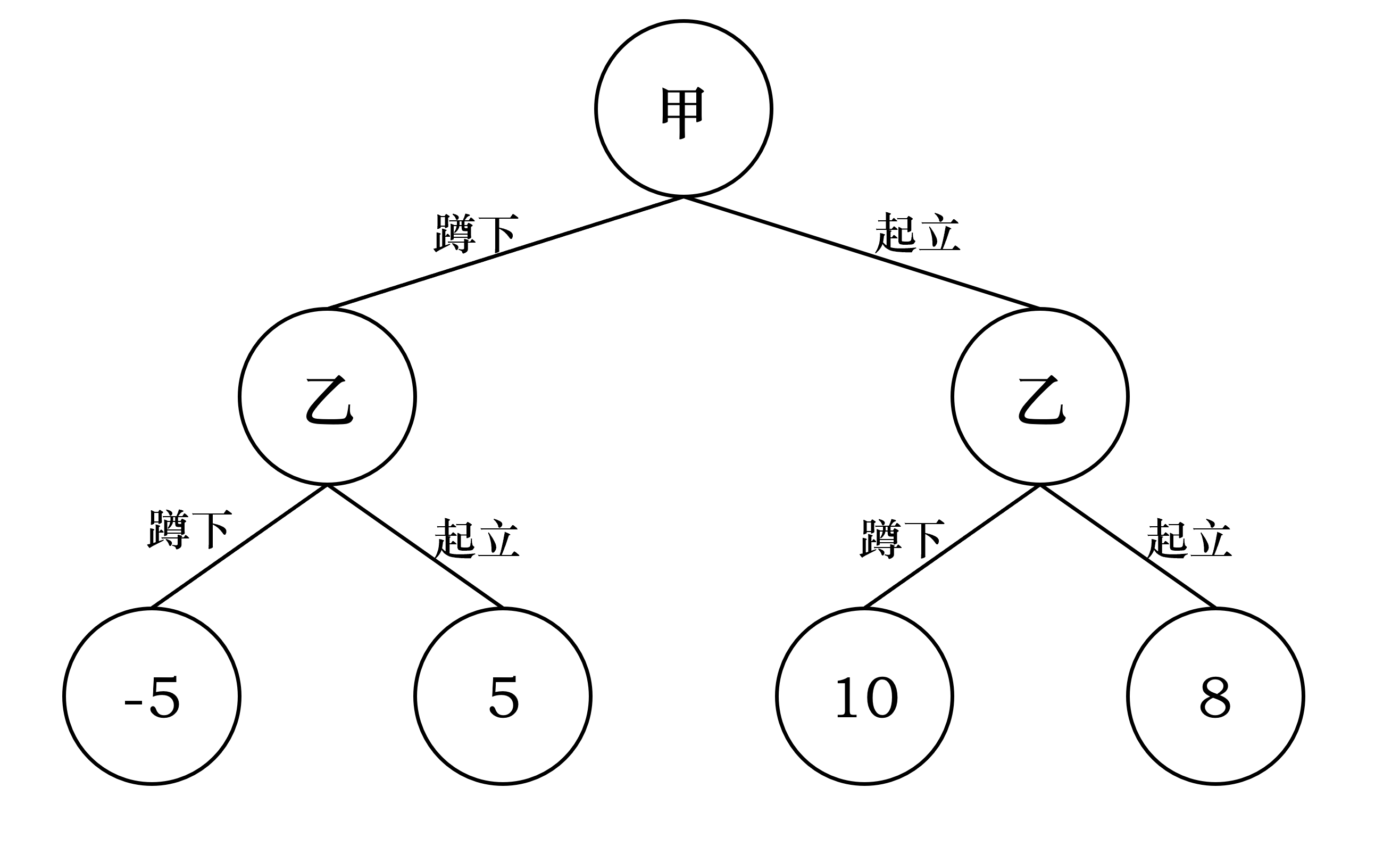
这棵树的起点通常称为根节点,树的末端通常称为叶节点,这棵树表示了博弈双方的收益,这就是博弈树
对于刚刚画出的这样一个博弈树,叶节点表示了博弈中甲方的收益,即叶节点表示了根节点一方的收益
以刚刚的博弈树为例,乙方在看到这样一颗树后,乙方应该怎么决策?
对于左边的子树,显然乙方蹲下甲方亏损5,乙方起立自己亏损5,对于乙方来说肯定选择叶节点的最小值-5;对于右边的子树同理,乙方要选择8让自己的亏损最小
使用极小化极大策略,甲方会在乙方决策的两个极小值中选择极大值,也就是8,让自己的收益在乙方亏损最小的情况下达到最大
Max层取值为子节点的最大值,表示最大化一方的收益最大
Min层取值为子节点的最小值,表示最小化一方的亏损最小

相比矩阵,博弈树可以表示多次决策,更方便地表示多步博弈的过程
博弈的目标
从初始状态(根节点)出发,寻找一条路径达到能赢的状态,本质是是一种搜索问题
搜索
树的遍历
搜索的基础是遍历,遍历即是对树中每一个节点进行一次且仅有一次的访问,而搜索是只寻找有利路径达到目标状态即停止
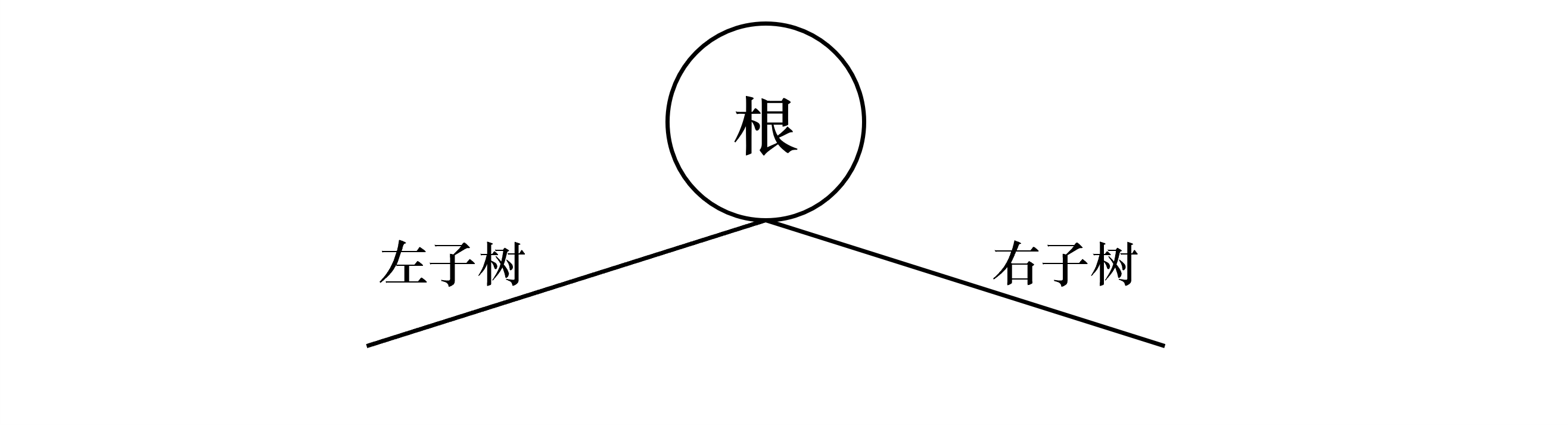
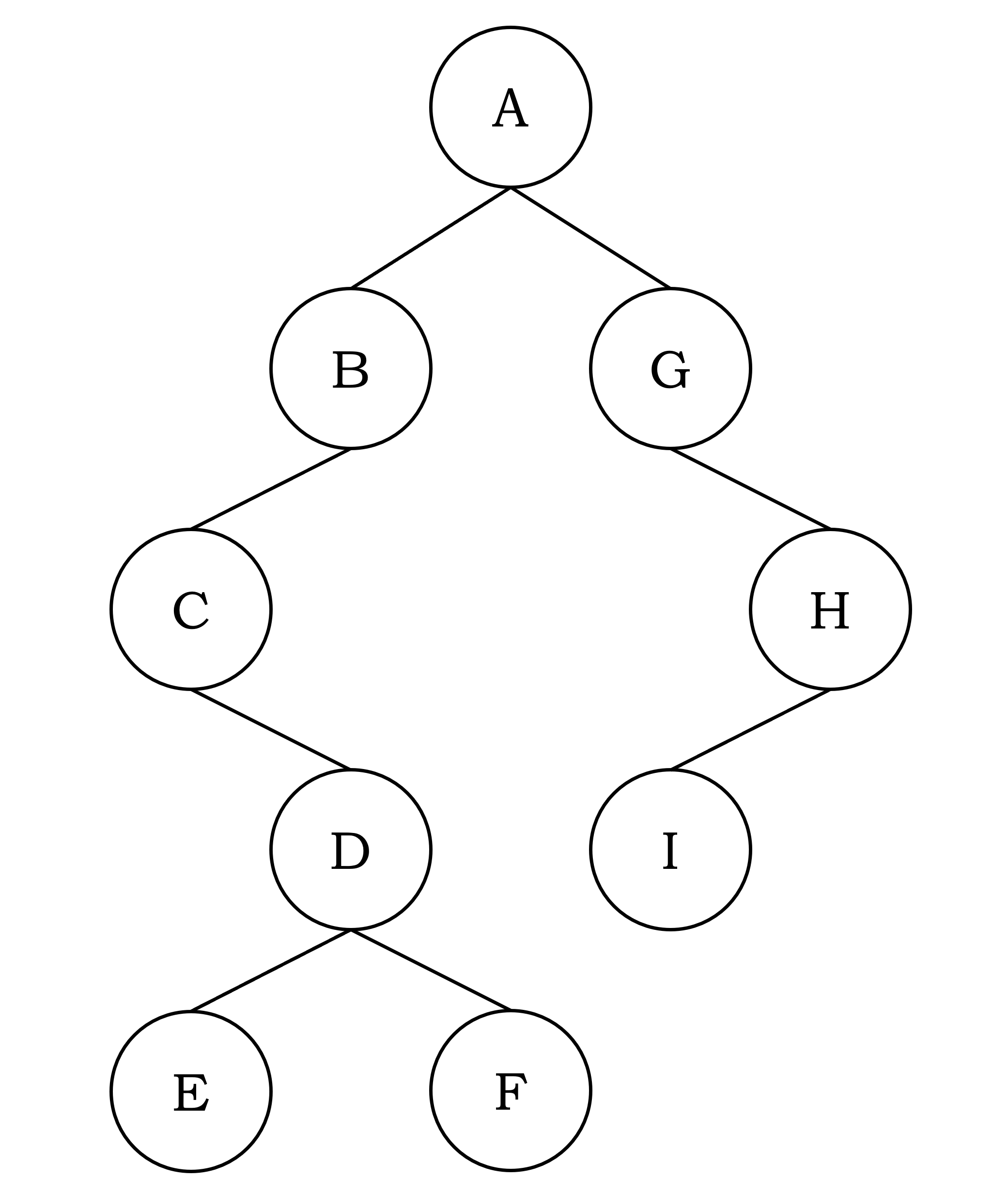
上图这样的树被称为“二叉树”,对于“树”共有三种不同的遍历方式,以下面这棵树为例 ——
前序遍历
顺序:根-左子树-右子树
每一层都要按照这个顺序进行遍历,以上面这棵树为例,按照前序遍历所输出的结果是
[根] [左子树] [右子树]
[A] [BCDEF] [GHI]
中序遍历
顺序:左子树-根-右子树
同样每一层都要按照这个顺序进行遍历,还以刚刚的那棵树为例:
[左子树] [根] [右子树]
[CEDFB] [A] [GIH]
后序遍历
顺序:左子树-右子树-根
同样每一层都要按照这个顺序进行遍历,还以刚刚的那棵树为例:
[左子树] [右子树] [根]
[EFDCB] [IHG] [A]
博弈树搜索
以3×3的井字棋为例,画出博弈树,这里省略了一些对称的棋局:

棋盘有9个位子,每个位子有3种状态,那么就一共有 $3^9 = 19683$ 种可能的棋局,$9! = 362880$ 种可能的博弈!
这只是9×9的棋局,再想想围棋,多模庞大的数字!如何进行有效的搜索?
让机器像人一样下棋 —— 以当前棋局向前看几步,用到一种方法评估,找到一种对当前最有利的走法
例如,我们要设计一个可以下井字棋的AI,首先就需要设计一个棋局评估函数来评估当前的棋局对机器的有利程度,然后进行有限深度的搜索(井字棋可以遍历所有可能,围棋当然不可能这样做),最后应用极小化极大策略确定如何落子
这也是几乎所有博弈问题的求解思路:设计棋局评估方法 -> 有限深度搜索 -> 寻找最优策略
这本质上是一种后序遍历的过程 —— 先得到各个子节点的评价值,再来计算当前节点的评价值,评价值的计算方法就是极大极小策略
α-β剪枝
α剪枝
在井字棋的例子中,可能的棋局数量已经非常少了,但还是不够少,极大极小策略中还隐含着可以进一步优化搜索的方法 ——
来看看这样一个例子:
刚刚提到,本质上是一种后序遍历的过程,那么程序需要先搜索左子树,
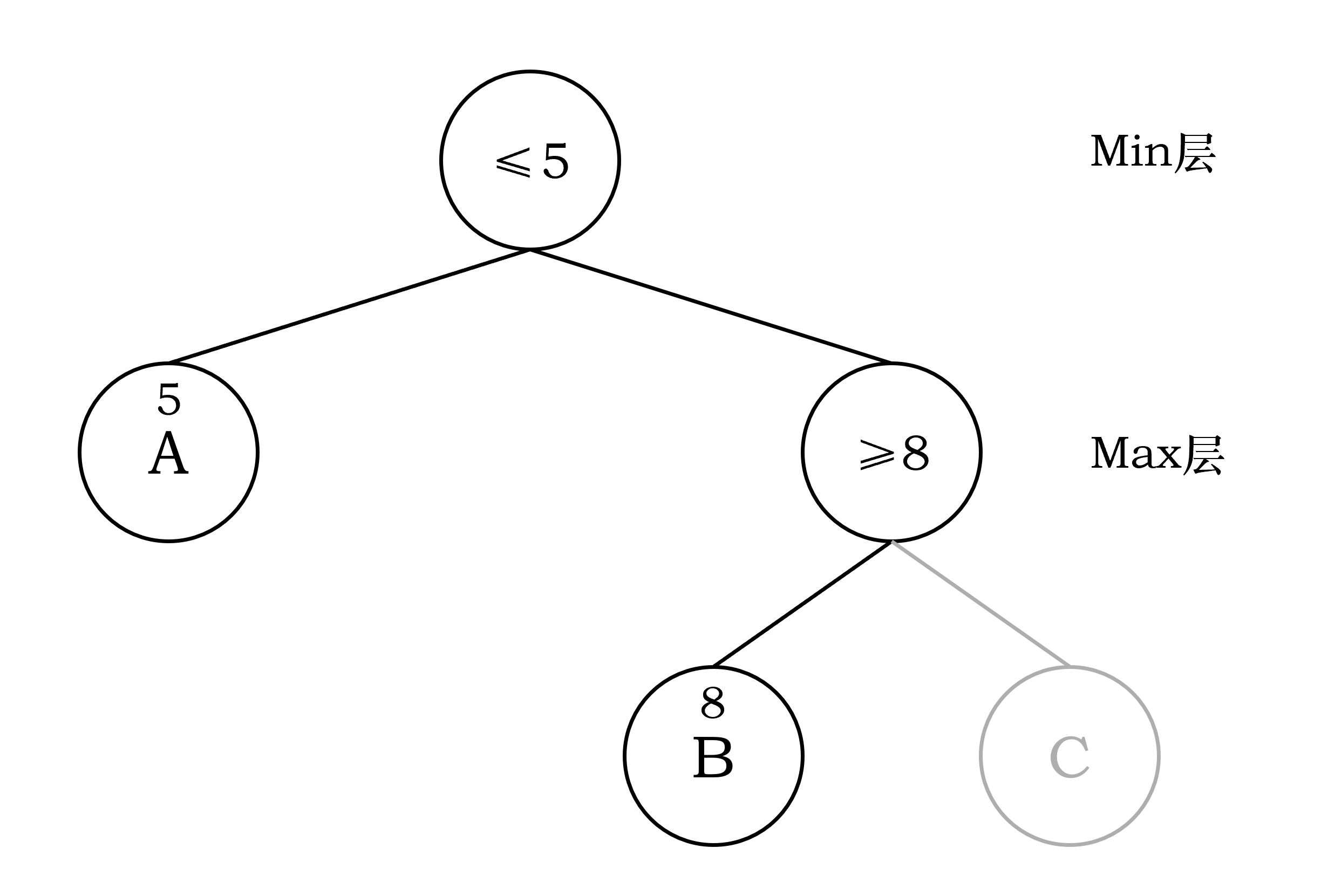
搜索左子树得到了左子树A节点的评估值为5,根据极小化极大策略,Max层根节点的评估值一定 $\ge 5$,这个“5”叫做“Max层节点的α值”(取当前子节点中最大评估值作为它评估值的下界)
再进行右子树的搜索,首先会搜索到右子树的B节点,计算得到的评估值为3。B节点上一层为Min层,这一层的取值要是子节点取值的最小值,即 $\le 3$。这个“3”叫做“Min层节点的β值”(取当前子节点中最小评估值作为它评估值的上界)
那么,我们可以轻易看出,因为B节点的存在导致C节点的评估值不可能大于5,C节点及其子树根本不需要考虑 —— 这就是α剪枝

β剪枝
同样的道理,还存在β剪枝:
若根节点是最小层,搜索左子树A得到5,那么根节点的值一定 $\le 5$
继续搜索右子树,搜索得到B节点的值为8,B节点的上一层为Max层取值为 $\ge 8$
同理,根节点为Min层,要求评估值 $\le 5$,右子树的C节点因为B节点的存在无论如何都不可能小于5,那么C节点及其子树同样看都不需要看 —— 这就是β剪枝
α-β剪枝
将两种剪枝方法同时应用,边搜索边计算α、β值进行剪枝:
α剪枝
任何Min层节点n的β值小于或定于它祖先节点的α值,则n以下的分支可以停止搜索,同时令节点n的评估值为β
β剪枝
任何Max层节点n的α值大于或等于它祖先节点的β值,则n以下的分支可以停止搜索,同时令节点n的评估值为α
这种方法,最大可以让搜索规模达到 $o(\sqrt{N})$ 个节点(N是博弈树节点的最大规模)
看到这里,恭喜你速通了深度搜索并掌握了α-β剪枝算法,你的人工智能图景又拼上了一块拼图
Ai8051U 运行深度搜索实现井字棋AI
棋盘定义
O表示机器(最大化玩家),X表示人(最小化玩家)
unsigned char board[BOARD_SIZE][BOARD_SIZE] = {
{' ', ' ', ' '},
{' ', ' ', ' '},
{' ', ' ', ' '}
};
棋盘状态判断
// 检查玩家是否获胜
unsigned char is_winner(char board[BOARD_SIZE][BOARD_SIZE], char player)
{
int i;
for (i = 0; i < BOARD_SIZE; i++)
{
// Check rows
if (board[i][0] == player && board[i][1] == player && board[i][2] == player) return 1;
// Check columns
if (board[0][i] == player && board[1][i] == player && board[2][i] == player) return 1;
}
// Check diagonals
if (board[0][0] == player && board[1][1] == player && board[2][2] == player) return 1;
if (board[0][2] == player && board[1][1] == player && board[2][0] == player) return 1;
return 0;
}
// 检查是否平局
unsigned char is_draw(char board[BOARD_SIZE][BOARD_SIZE])
{
int i,j;
for (i = 0; i < BOARD_SIZE; i++)
{
for (j = 0; j < BOARD_SIZE; j++)
{
if (board[i][j] == ' ') return 0;
}
}
return 1;
}
极小化极大算法
注意:在C51中,如果函数需要递归调用,需要加上 reentrant 可重入修饰符
// 极小化极大算法
int minimax(char board[BOARD_SIZE][BOARD_SIZE], int depth, int is_maximizing, int alpha, int beta) reentrant
{
int i, j, score, best_score;
unsigned char new_board[BOARD_SIZE][BOARD_SIZE];
// 若传入的棋局已经有人获胜,则返回评估值
if (is_winner(board, 'X')) return -1;
if (is_winner(board, 'O')) return 1;
if (is_draw(board)) return 0;
if (is_maximizing) // 若当前是最大化玩家(○)
{
best_score = -INFINITY;
for (i = 0; i < BOARD_SIZE; i++)
{
for (j = 0; j < BOARD_SIZE; j++)
{
if (board[i][j] == ' ')
{
board[i][j] = 'O';
copy_board(board, new_board);
score = minimax(new_board, depth + 1, 0, alpha, beta);
board[i][j] = ' ';
best_score = (score > best_score) ? score : best_score; // 更新最佳评估值
if (score > alpha) alpha = score; // 更新α值
if (alpha >= beta) break; // 如果α值已经大于等于β,剪枝
}
}
if (alpha >= beta) break; // 如果α值已经大于等于β,剪枝
}
return best_score;
}
else // 若当前是最小化玩家(×)
{
best_score = INFINITY;
for (i = 0; i < BOARD_SIZE; i++)
{
for (j = 0; j < BOARD_SIZE; j++)
{
if (board[i][j] == ' ')
{
board[i][j] = 'X';
copy_board(board, new_board);
score = minimax(new_board, depth + 1, 1, alpha, beta);
board[i][j] = ' ';
best_score = (score < best_score) ? score : best_score; // 更新最佳评估值
if (score < beta) beta = score; // 更新β值
if (alpha >= beta) break; // 如果α值已经大于等于β,剪枝
}
}
if (alpha >= beta) break; // 如果α值已经大于等于β值,剪枝
}
return best_score;
}
}
在 minimax 函数中,以下部分充当了“棋局评估函数”:
if (is_winner(board, 'X')) return -1;
if (is_winner(board, 'O')) return 1;
if (is_draw(board)) return 0;
使用嵌套的循环生成博弈树的子节点,递归调用 minimax 函数评估子节点,利用α值、β值进行剪枝减小计算量
先手玩家的决定
利用了 Ai8051U 的高速真12位ADC通道采集电压,随机决定。
下面是 ADC 采样的代码
int Get_ADC12bitResult(unsigned char channel) // channel = 0~15
{
ADC_RES = 0;
ADC_RESL = 0;
ADC_CONTR = (ADC_CONTR & 0xf0) | channel; // 设置ADC转换通道
ADC_START = 1; // 启动ADC转换
while(ADC_FLAG == 0); // 等待ADC完成
ADC_FLAG = 0; // 清除ADC结束标志
return (((u16)ADC_RES << 8) | ADC_RESL);
}
void main()
{
unsigned char current_player, first_hand;
first_hand = current_player = Get_ADC12bitResult(7) % 2 == 0 ? 'X' : 'O';
}
开源
程序库中的SP.2. 井字棋AI
 附件:SP.2. 井字棋AI.zip
附件:SP.2. 井字棋AI.zip
开发板及例程均使用 MIT License 协议开源
参考
华为《搜索与人工智能》课程
 |手机版|深圳国芯人工智能有限公司
( 粤ICP备2022108929号-2 )
|手机版|深圳国芯人工智能有限公司
( 粤ICP备2022108929号-2 )