[i=s] 本帖最后由 fangs 于 2024-12-3 16:53 编辑 [/i]<br />
<br />
本文以非正式的语言叙述了神经网络的构建，所述内容仅供入门，可能与论文、书籍存在出入。
如果你了解线性代数与微积分相关知识，可以更好理解本文，但阅读本文不需要任何线性代数与微积分相关知识。
神经网络入门
什么是神经网络？
这里有一个方程，你可以把鳄鱼或者蛇的身长$x_1$和体重$x_2$代入下面的方程，方程的结果就能告诉你这是鳄鱼还是蛇：
$$
-1.4x_1 + 2.3x_2 + 200 = y
$$
如果输出结果y>0表示这是鳄鱼，输出结果y<0表示这是蛇。
例如：眼镜王蛇的身长是359，体重是6，输出结果是-288.8，是蛇
例如：尼罗鳄的身长是316，体重是137.5，输出结果是73.85，是鳄鱼
这就是一个最简单的神经元，神经网络的本质就是分类
下面这张图就是可以分类鳄鱼和蛇的神经元，神经元接受两个信号，分别有着不同的权重，计算结果与阈值相比较，决定这个神经元的输出
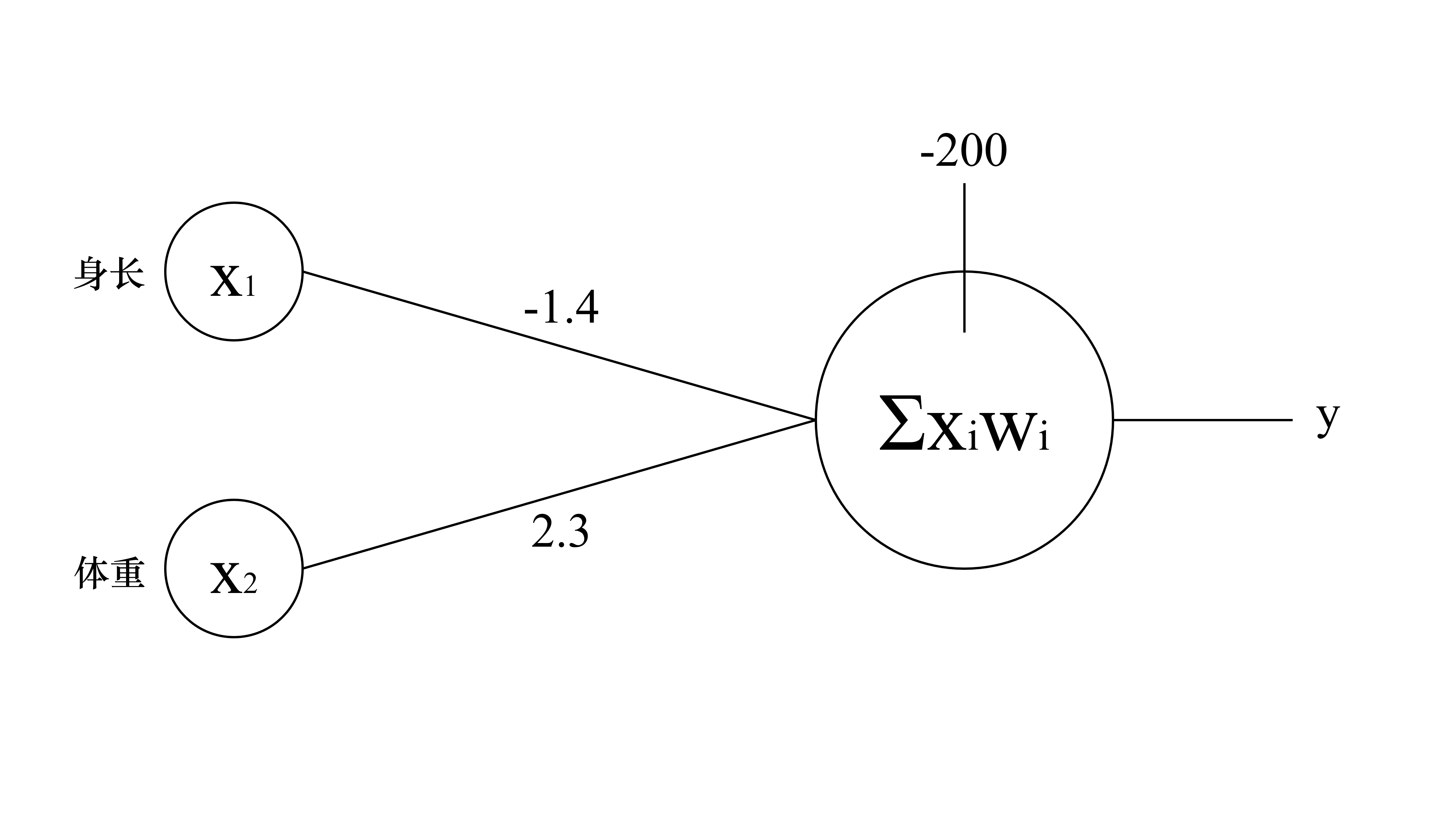
通常情况，一个神经元的输入有很多，就像这样——
$$
x_1 w_1 + x_2 w_2 +... + x_n w_n + b = y
$$
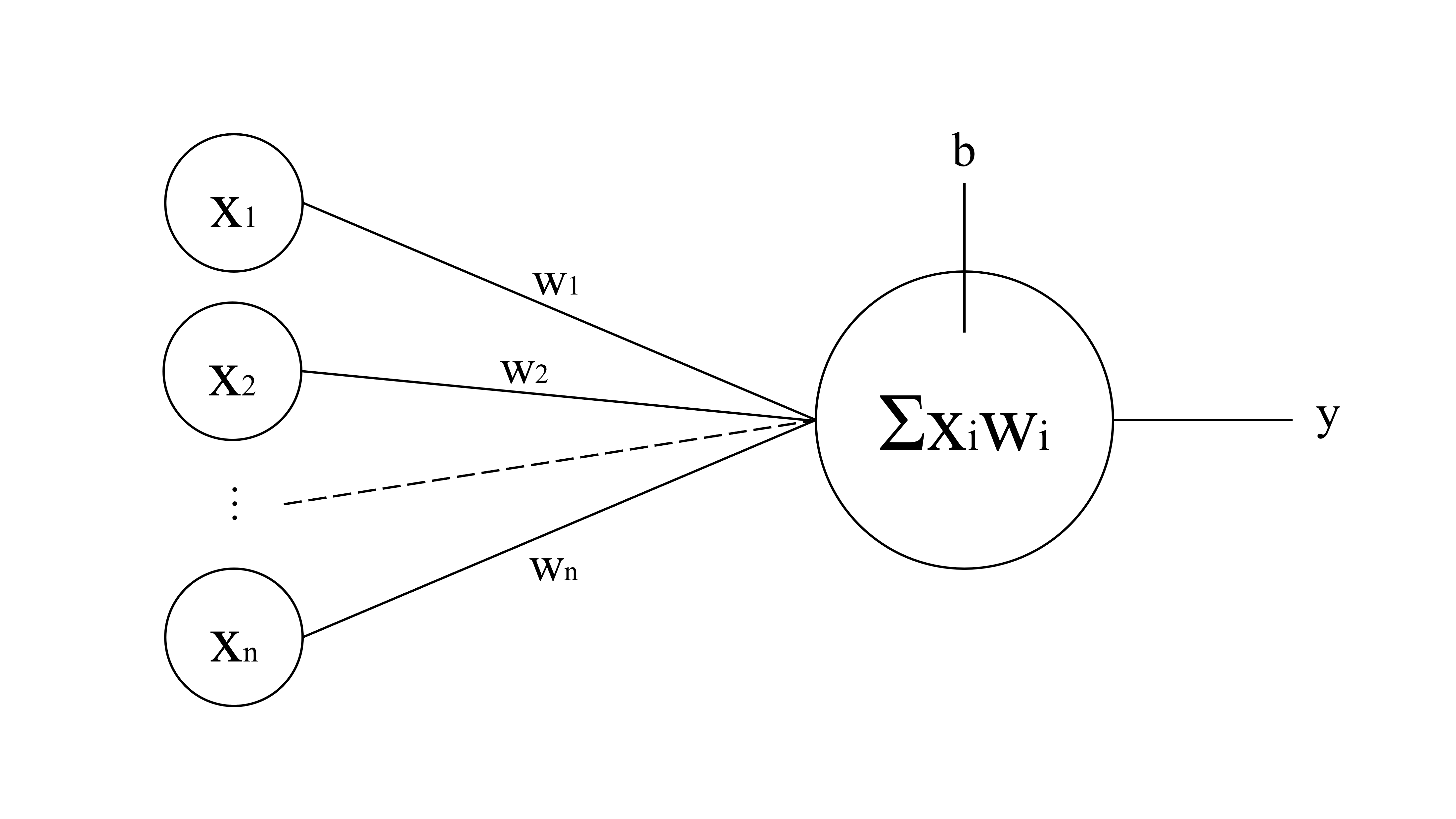
神经网络就由许许多多的像这样的神经元构成
结构是这样，那么当给出一些数据，例如鳄鱼和蛇的身长、体重数据，如何让机器自动调整$w$？
机器怎么学习？
给定鳄鱼和蛇的身长、体重数据，神经元的结构是$x_1w_1 + x_2w_2+200=y$，怎么自动调整$w_1$和$w_2$？这个过程就是机器学习
理论上只要不断改变$w_1$和$w_2$就能把鳄鱼和蛇分类成功，每次迭代，可以描述为这样：
$$
w{i(t+1)} = w{i(t)} + \Delta w_i
$$
不难看出，只要选定一个靠谱的$\Delta w_i$计算公式，那么机器就能自动学习
这里假设当$\Sigma x_i w_i > b$输出$y=1$表示鳄鱼，反之输出$y=0$表示蛇，预期结果是$Y$
不难看出，预期结果$Y$和输出结果$y$，可以让机器知道输出的结果是否正确，那么可以构建一个式子，依赖这个式子，就可以根据输出结果自动调整$w$：
$$
\Delta w_i = (Y-y)\times x_i
$$
在真实情况下，阈值$b$也会像$w$这样调整，完整是式子是这样的——
$$
\begin{matrix}
\Delta w_i = (Y-y)\times x_i\times r \
\Delta b = (Y-y)\times 1\times r
\end{matrix}
$$
$r$是什么？你先别急，试试下面这个例子
扭曲空间！
在刚刚，你成功让机器学习了如何分类鳄鱼和蛇，那来试试这个——分类蓝色[$(1,0)$和$(0,1)$]和黄色圆点[$(0,0)$和$(1,1)$]
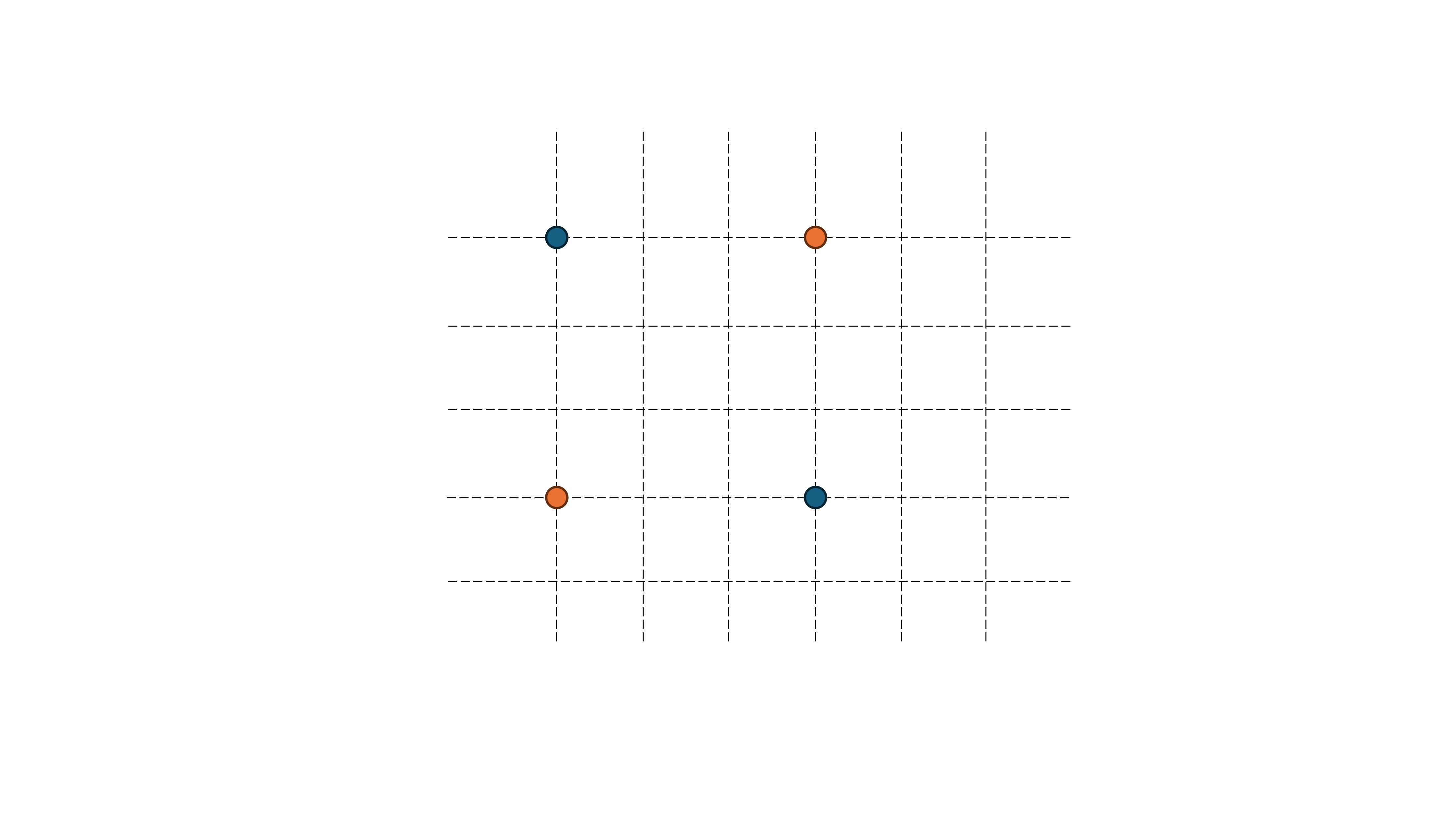
分不开！怎么想都分不开吧！果能弯曲这条分割线，那就好办了
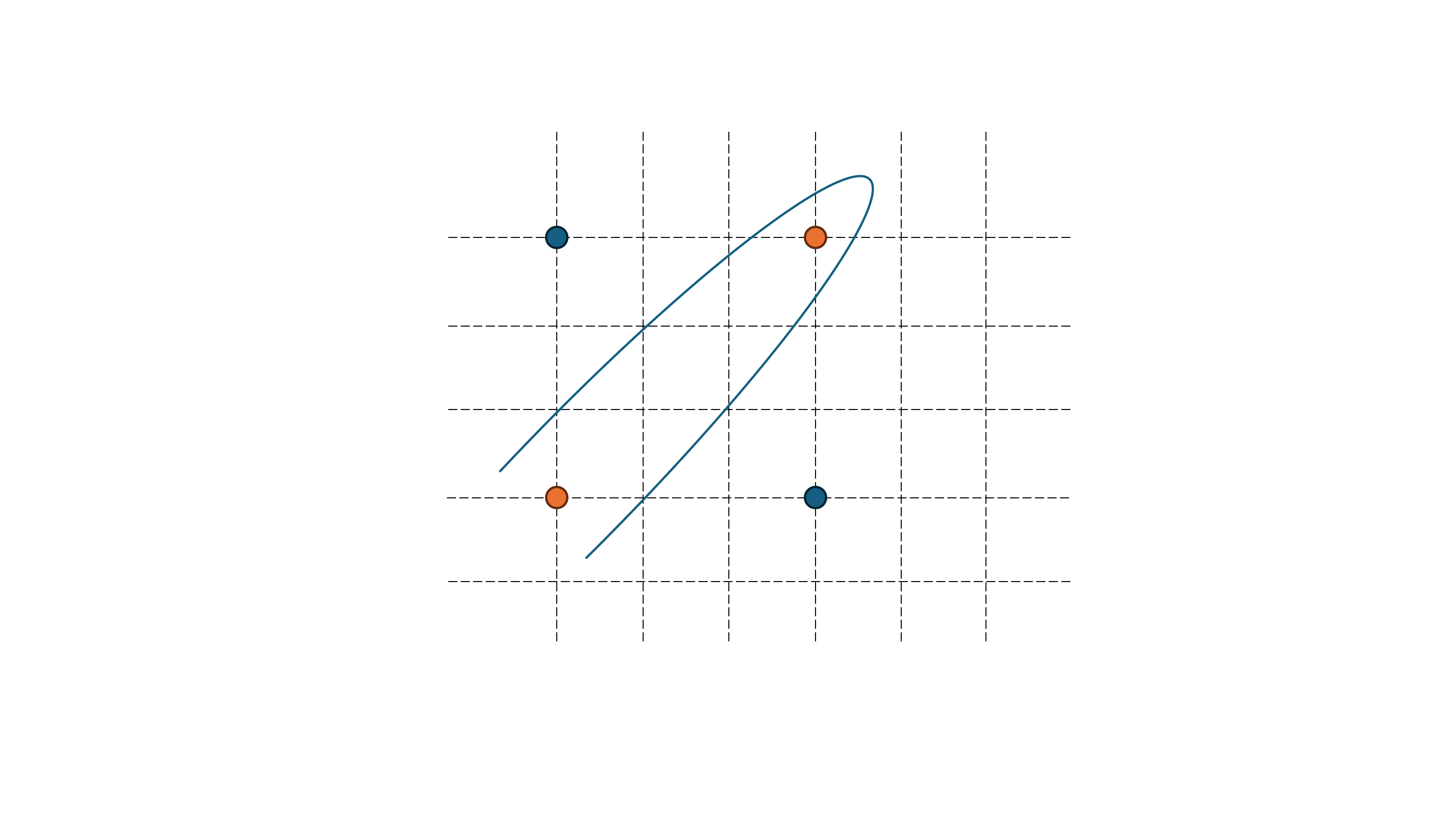
很可惜！因为输入数据$x$是一次的，那么输出和输入的关系就是一次函数，体现在二维平面就一定是一条直线
作为一个生活在三维中的人，可以试试降维打击 —— 扭曲这个二维平面，那么就能分开这四个点了：
还以刚刚分类鳄鱼和蛇的例子，为了弯曲平面，需要在输入层与输出神经元之间增加一个隐藏层
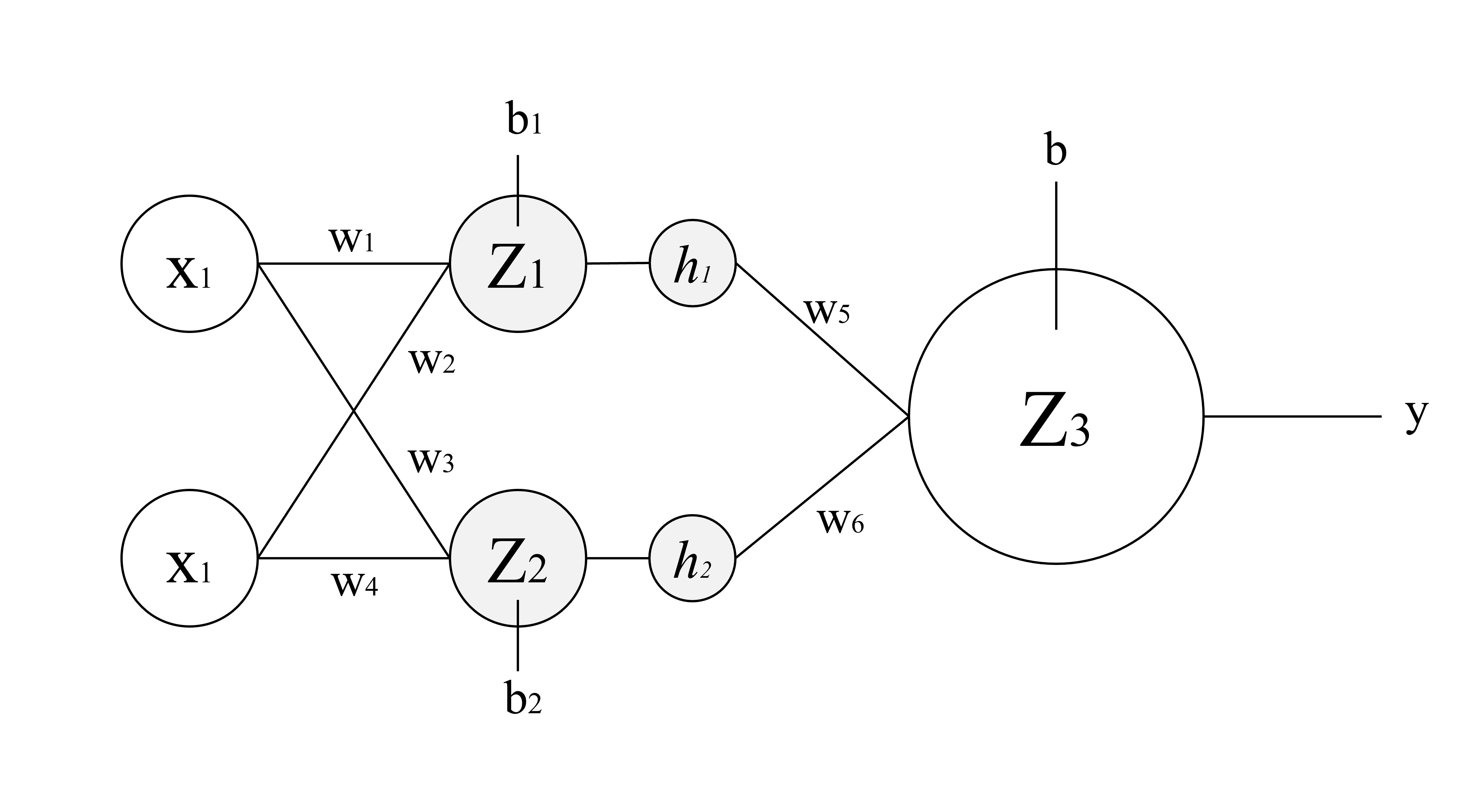
在一开始，这个二维平面，横坐标是$x_1$纵坐标是$x_2$，加一层后就变成了$z_1$和$z_2$
输入神经元的值就变成了 $z_1 = w_1x_1+w_2x_2+b_1$ 和 $z_2 = w_3x_1+w_4x_2+b_2$
你可以算算看，调整$w_1,w_2,w_3,w_4$可以将原来的平面映射到一个新的平面——
调整$w_1$可以在水平方向上伸缩甚至翻转坐标系
调整$w_4$可以在垂直方向上伸缩甚至翻转坐标系
调整$w_2$可以让纵轴倾斜
调整$w_3$可以让横轴倾斜
调整$b_1$可以在水平方向上平移坐标系中的点
调整$b_2$可以在垂直方向上平移坐标系中的点
很有趣对吧！现在，你再试试调整这个模型中的权重和阈值分开本节开头的那四个点！
你可以鼠标选中下面的黑条查看答案
<span style="background: black; color: black;">别试了，是分不开的</span>
<span style="background: black; color: black;">这个变换本质上还是线性变换，怎么办？加一层非线性变换就好了</span>
隆重介绍——激活函数
让隐藏层的两个神经元的输出值经过可以对整个空间非线性变换的激活函数$h$后再输入输出神经元
激活函数是可以让输入数据以一种更规律的方式输出的规则
在鳄鱼和蛇的例子中，输出值大于0是鳄鱼、小于0是蛇，本质上就是一种阶跃函数
$$
\varepsilon (x)=\left{\begin{matrix}1 & x\ge 0 \0 & x < 0\end{matrix}\right.
$$
除了阶跃函数，还有双曲正切函数$\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} $、逻辑函数$\sigma (x) = \frac{e^x}{e^x + 1} $以及线性整流函数$ReLU(x)=\left{\begin{matrix} x & x>0 \0 & x \le 0\end{matrix}\right.$
有了激活函数这么强有力的工具，现在，你就可以修改这个神经网络，完成上一节哪个不可能的任务了！
这里以线性整流函数$ReLU(x)=\left{\begin{matrix} x & x>0 \0 & x \le 0\end{matrix}\right.$为激活函数$h$：
这样，就将那四个点完成了分类，从上向下看变换后的平面，它长这样：
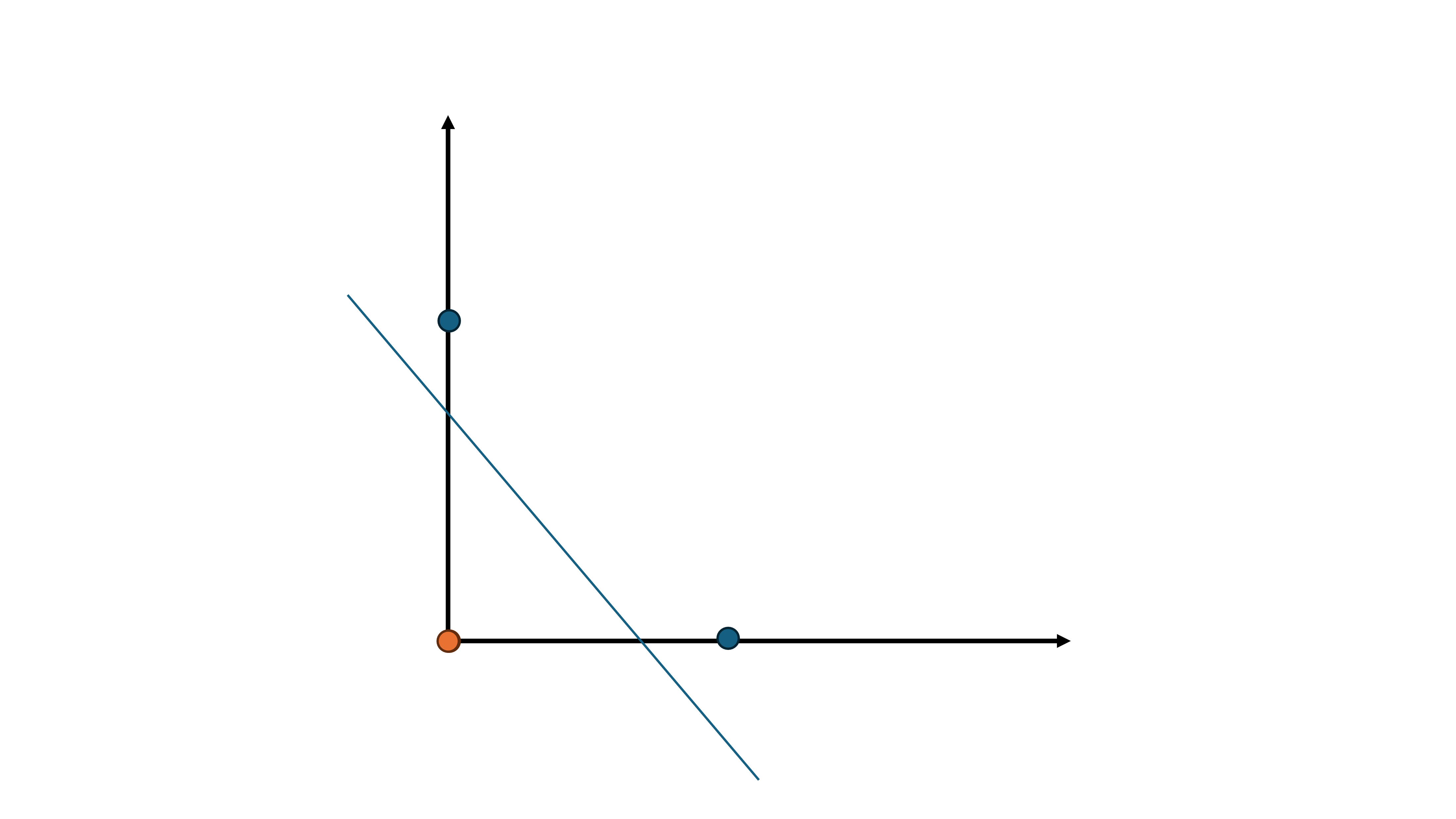现在，来挑战分开这个吧！
<span style="background: black; color: black;">别试了，其实还是分不开的</span>
降维打击
如果提升一个维度，就容易得多了，在隐藏层增加一个神经元，那么就增加了一个维度
提升维度后，分割数据的不再是一条线，而是一个面
这个你就别算了，直接告诉你：可以通过调整权重、激活函数将黄点聚集在一起，就像下面这个图一样：
很抽象对吧？就像将二维平面揪起了一个角，这些黄点聚集在角上
梯度下降
理论上有了刚刚这个模型，可以完成所有的分类问题，但难题是：怎么让机器自己调整这些阈值？
以刚刚这个较为简单的模型为例，假设神经元$Z_3$输出结果需要经过阶跃函数$\varepsilon (x)$，输出值1表示蓝点、输出值0表示黄点
现在，令其所有的权重与阈值都为0，计算输出结果
那么就有了一张这样的表格，记录模型预测的准确情况，将$|Y-y|$记为误差
| 输入$(x_1,x_2)$ |
目标$Y$ |
输出$y$ |
误差$Cost$ |
| (0,1) |
1 |
1 |
0 |
| (1,0) |
1 |
1 |
0 |
| (1,1) |
0 |
1 |
1 |
| (0,0) |
0 |
1 |
1 |
将$\frac{1}{N}\Sigma |Y-y|$定义为模型误差：误差越低，模型越准确（例如，当前这个模型的误差为 0.5）
这个模型误差受$w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b$共9个变量影响，这就是损失函数
$$
Cost = \frac{1}{N}\Sigma |Y-y| = f(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b)
$$
在常见的机器学习里，为了便于计算，会变为这样
$$
Cost = \frac{1}{2N}\Sigma |Y-y|^2 = f(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b)
$$
在机器学习中，核心目标就是让损失函数越低越好，如何找到损失函数的最低点？
使用梯度下降算法可以找到损失函数最低的那一点
以二次函数$y=x^2$为例，我们的目标是让无论处在何处的A点自动找到二次函数的最低点
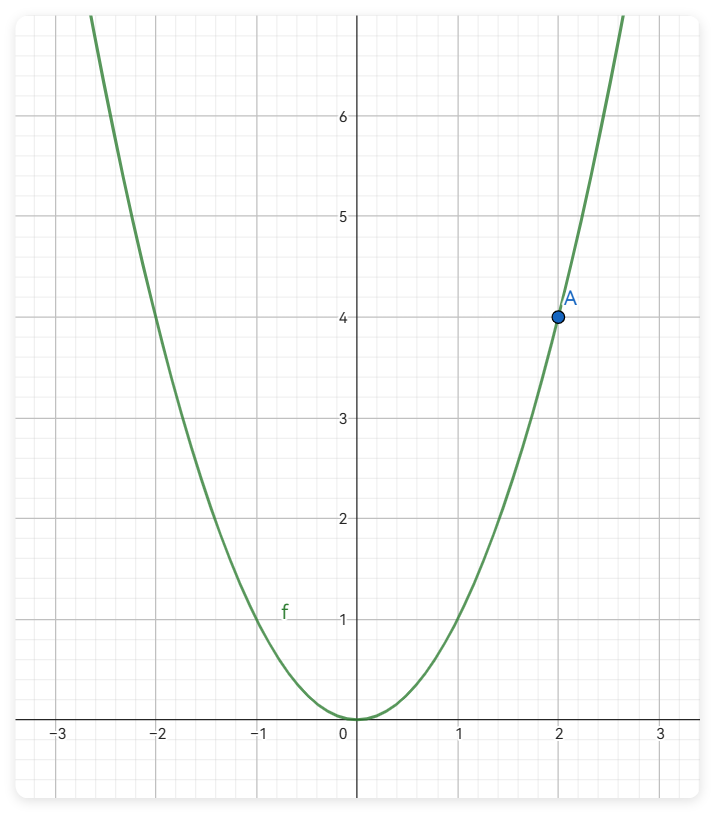
仔细想想，只需要知道A点下一步在横坐标的移动方向和距离，就可以找到二次函数的最低点了
对于A点的移动方向：A点所在处的斜率为正，那么就应该让A点向负方向移动，反之亦然
对于A点的移动距离：以当前点的梯度为参考，决定移动的距离，可以高效准确地找到最低点
细心的你可能会发现，在某些点，例如$(2.5，6.25)$这个点梯度为5，下一个点会移动到$(-2.5，6.25)$，梯度是-5，这个点会在$(2.5，6.25)$和$(-2.5，6.25)$之间反复横跳
再引入一个新的变量来决定A点的移动距离，就避免了可能存在的这种会导致反复横跳的点
现在，让$移动距离=梯度×比例$，选取一个合适的比例就可以解决反复横跳的问题
这个比例就是步长，也就是在第一节末尾的$r$，在机器学习中称为学习率
这就是让机器找到损失函数最低点的方法：
- 根据梯度寻找移动方向
- 根据梯度和学习率确定移动距离
- 多次迭代
在多维空间中也是同样道理，对于损失函数
$$
c = \frac{1}{2N}\Sigma |Y-y|^2 = f(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b)
$$
求得
$$
\frac{\partial c}{\partial w_1} ,\frac{\partial c}{\partial w_2} ,\frac{\partial c}{\partial w_3} ,\frac{\partial c}{\partial w_4} ,\frac{\partial c}{\partial w_5} ,\frac{\partial c}{\partial w_6} ,\frac{\partial c}{\partial w_7} ,\frac{\partial c}{\partial b_1} ,\frac{\partial c}{\partial b_2} ,\frac{\partial c}{\partial b}
$$
只需要对大量参数疯狂求导，利用这些偏导数就可以找到梯度下降的方向
终点
将刚刚的这些拼在一起——输入层、中间层、激活函数、输出层，通过损失函数找到权重与阈值的最优解，就是人工智能的源头——神经网络了
在 Ai8051U 上运行神经网络
回忆一下刚刚构建的神经网络模型，
需要完成的任务是对 8*8 的像素点阵进行预测，那么就有64个输入，再选择隐藏层的大小、激活函数，就可以完成预测手写数字的任务
为了能让你更好理解，在这里我们要自己构建一个数据集
构建数据集
8x8 的点阵可以看作一个长度为64的一维数组，每个元素都是点阵中的一个点。用0表示空白，1表示黑色笔画（事实上，真实的手写数字识别还需要考虑笔画灰度的影响，这里不考虑灰度）
数字2可以表示成这样：
[
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 0, 0, 0,
0, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0
]
这里的每一个元素，都是特征，就像鳄鱼和蛇的例子中的身长和体重
在刚刚神经网络的入门中以及了解过机器学习的核心是损失函数，损失函数的定义包括了预期输出，在构建数据集时还要加上预期输出来告诉机器预测的是否正确，这里以 json 储存数据集：
[
{
"label": "2",
"data": [
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 0, 0, 0,
0, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0
]
}
]
这里的 label是预期结果，也就是分类标签，在最开始提到过神经网络的本质是分类，那么这个模型要预测从0到9的数字，输出分类就有10种
有了数据集，就可以构建神经网络模型开始训练了
训练神经网络
等等，你不会真的想手搓神经网络吧？有许多软件都可以完成神经网络的构建和训练，完全可以使用现成的软件，而不是重复造轮子
以scikit-learn为例，scikit-learn（简称sklearn）是一个开源的Python机器学习库，下面将使用Python一步一步编写神经网络训练程序
读取数据集
# 读取 JSON 文件
with open('data.json', 'r') as file:
data = json.load(file)
# 提取特征和标签
X = np.array([item['data'] for item in data])
y = np.array([item['label'] for item in data])
分割测试集
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1089890203)
random_stat 是随机种子，保证结果的可重复性
定义神经网络模型
# 定义神经网络模型
mlp = MLPClassifier(hidden_layer_sizes=(8, 8), max_iter=500, random_state=1089890203, learning_rate_init=0.005)
hidden_layer_sizes 表示隐藏层的大小，这里有两个隐藏层，每层有8个神经元
max_iter是训练过程中的最大迭代次数
random_state 是随机种子，保证结果的可重复性
learning_rate_init 是初始学习率
默认的激活函数是线性整流函数$ReLU(x)=\left{\begin{matrix} x & x>0 \0 & x \le 0\end{matrix}\right.$
所以，这个神经网络总共有3层：一个输入层，两个隐藏层，以及一个输出层。
输入层有64个特征，隐藏层0有8个神经元，隐藏层1有8个神经元，输出层有10个类别
训练模型
# 训练模型
mlp.fit(X_train, y_train)
使用测试集试验模型准确度
# 在测试集上进行预测
y_pred = mlp.predict(X_test)
输出日志
# 输出分类报告
print(classification_report(y_test, y_pred, zero_division=1))
# 输出混淆矩阵
cm = confusion_matrix(y_test, y_pred)
print("混淆矩阵:")
print(cm)
# 输出训练的准确率
accuracy = mlp.score(X_test, y_test)
print("准确率: {:.2f}%".format(accuracy * 100))
输出各层参数到文件
为了能将神经网络部署到 Ai8051U，需要得到这个神经网络具体的参数
# 各个神经元的参数
nn_parameters = {}
for i, layer_weights in enumerate(mlp.coefs_):
nn_parameters[f"Layer {i} weights"] = layer_weights.tolist()
# 将神经网络的参数输出到文件
with open('neural_network_parameters.json', 'w') as f:
json.dump(nn_parameters, f, indent=4)
到这里，就完成了神经网络的训练，下面只需要把神经网络部署到 Ai8051U 就行了
部署到 Ai8051U
注意！这里的前向传播函数并不是所有神经网络通用的，只使用于本文的模型
程序
将刚刚得到的神经网络参数储存到 nn.h
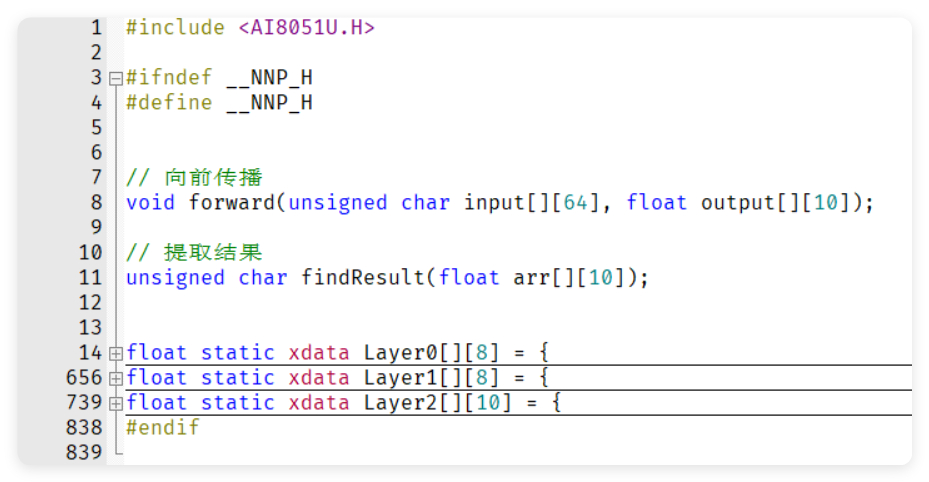
在 nn.c 编写神经网络的程序
// 激活函数
float relu(float x) {
return (x > 0) ? x : 0;
}
// 向前传播
void forward(unsigned char input[][64], float output[][10])
{
float layer0Output[][8] = {{0}};
float layer1Output[][8] = {{0}};
float sum;
unsigned char i, j, k;
for(i = 0; i < 1; i++)
{
for(j = 0; j < 8; j++)
{
sum = 0;
for(k = 0; k < 64; k++)
{
sum += input[i][k] * Layer0[k][j];
}
layer0Output[i][j] = relu(sum);
}
}
for(i = 0; i < 1; i++)
{
for(j = 0; j < 8; j++)
{
sum = 0;
for(k = 0; k < 8; k++)
{
sum += layer0Output[i][k] * Layer1[k][j];
}
layer1Output[i][j] = relu(sum);
}
}
for(i = 0; i < 1; i++)
{
for(j = 0; j < 10; j++)
{
sum = 0;
for(k = 0; k < 8; k++)
{
sum += layer1Output[i][k] * Layer2[k][j];
}
output[i][j] = relu(sum);
}
}
}
// 提取结果
unsigned char findResult(float arr[][10]) {
unsigned char i;
float max = arr[0][0];
unsigned char maxIndex = 0;
for (i = 1; i < 10; i++) {
if (arr[0][i] > max) {
max = arr[0][i];
maxIndex = i;
}
}
return maxIndex;
}
在向前传播中进行了三次矩阵乘法，分别是：
$$
\begin{matrix}
[layer0Output] = [input] \times [Layer0] \
[layer1Output] = [layer0Output] \times [Layer1] \
[output] = [layer1Output] \times [Layer2]
\end{matrix}
$$
调用
unsigned char input[][64] = {{0}};
float output[][10] = {{0}};
unsigned char result = 0;
void INT0_int(void) interrupt 0
{
P17 = 1;
forward(input, output);
result = findResult(output);
P17 = 0;
}
例子
input
{{
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 0, 0, 0,
0, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0
}};
layer0Output
{{
1.7427662894678484,
3.7626030058712647,
0,
3.283818020187059,
2.154583433576627,
0.15074766629823577,
3.0851679342759692,
1.0029153854424906
}}
layer1Output
{{
5.28526589778266,
7.5431893188351715,
0,
0,
12.371341248962006,
3.653461801195259,
2.5893509258389504,
0.48358559289200287
}}
output
{{
0,
0.6895957996723958,
17.517413428468885,
12.60312725756366,
0.4306102331979812,
0,
1.862949802924105,
0,
0,
0
}}
亲自试试
看到这里，你应该不需要我提供完整源代码就能复刻了，一定要亲自试试
我开发了一个网页，你可以在这里制作属于你的数据集，或者试试我的神经网络：
https://dev.miri.site/ai8051u-nn/
当然，由于为了可以在 mcu 运行牺牲了许多神经元，再加上数据集不够广泛，预测结果可能并不正确
如果你想要自己制作数据集：先打开开发者工具（按F12）进入控制台，在输入框中输入分类标签，点击Save，你会发现控制台输出了一个 JavaScript 对象，它就是 Json 格式的数据集，你可以右键复制它
开源
如果不想动手自己试着做一个，也可以在我的例程库找到全部源码：SP.1. 神经网络
https://github.com/klxf/Ai8051U-Samples/
附件：SP.1. 神经网络.zip
以MIT协议开源
参考
- 一个人工智能的诞生
- 机器学习-梯度下降算法原理及公式推导_梯度下降计算公式-CSDN博客
- Gradient-Descent（全世界最通俗易懂的梯度下降法详解-优化函数大法） - 知乎
- 神经网络基础内容--输入、隐藏、输出三层及激活、损失、优化函数简单介绍 - 知乎
|手机版|小黑屋|深圳国芯人工智能有限公司
( 粤ICP备2022108929号-2 )
已绑定手机
发表于 2024-12-3 12:12:58
发表于 2024-12-3 16:52:07